Data Structures 101: Binary Search Trees
A simple guide to understanding the Binary Search Tree 🌲
Assalam u Alaikum & hello everyone! 👋🏻✨
I hope you all are doing well. In the previous post about the Introduction To Trees, we learned what are trees, different types of trees and finally, we implemented a simple general tree using JavaScript.
In this post, we are going to learn a very famous type of tree that is Binary Search Tree
✨ Contents
- What is a Binary Search Tree?
- Applications Of Binary Search Tree
- Time and Space Complexity
- Implementation Of Binary Search Using JavaScript
NOTE: This post requires some basic knowledge of Tree Data Structure. If you are not familiar with Tree Data Structure, I recommend you to please read my previous post: Introduction to Trees
🌲 What is a Binary Search Tree?
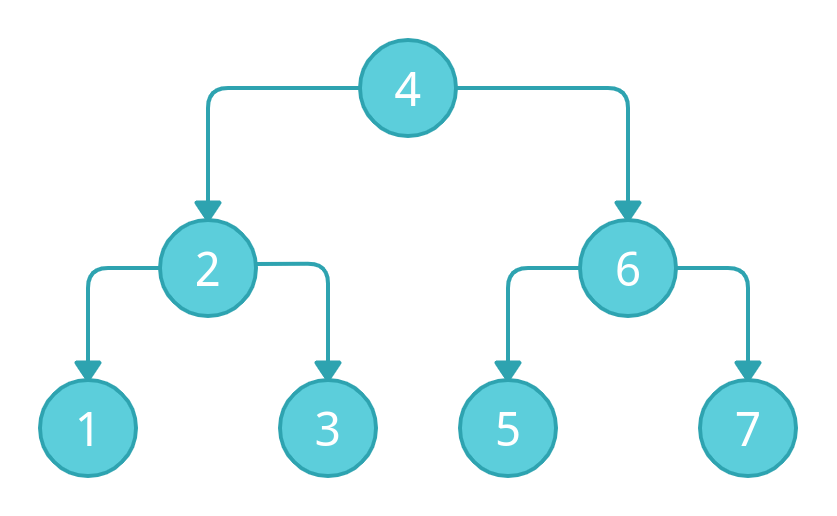
A Binary Search Tree is a form of a Binary Tree with the following restrictions:
- The left child value of a node should be less than or equal to the parent value.
- The right child value should always be greater than or equal to the parent’s value.
- The left and right subtrees must also be a binary search tree.
🌲 Applications Of Binary Search Tree
An ideal way to go with the hierarchical way of storing data.
Make insertion and deletion faster than linked lists and arrays.
Since BST follow a structure for inserting the records, the search operation becomes very efficient. Thus, this tree is heavily used in applications where searching is a primary function.
Used in sorted streams of data.
TreeMap and TreeSet data structures are internally implemented using self-balancing BSTs.
🌲 Time and Space Complexity
Let's take a look at the time complexity of BST.
| Operation | WorstCase | Average Case |
| Search | O(n) | O(log n) OR O(h) |
| Insert | O(n) | O(log n) OR O(h) |
| delete | O(n) | O(log n) OR O(h) |
Where h = height of tree
🌲 Understanding the Time Complexity
Since the time complexity is the same for all the operations, both in worst and average cases. Let's understand how it's the same for all the operations.
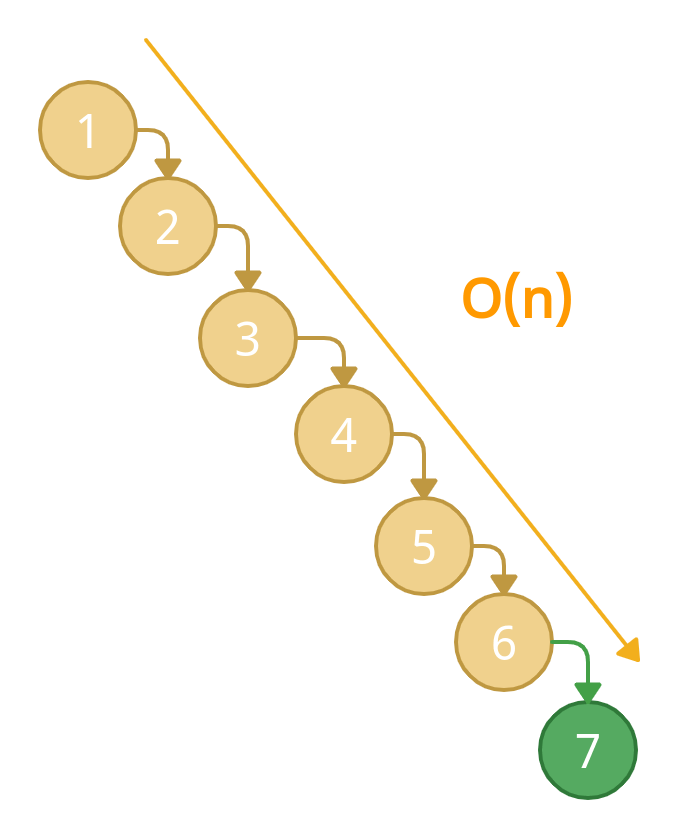
🤯 Worst Case
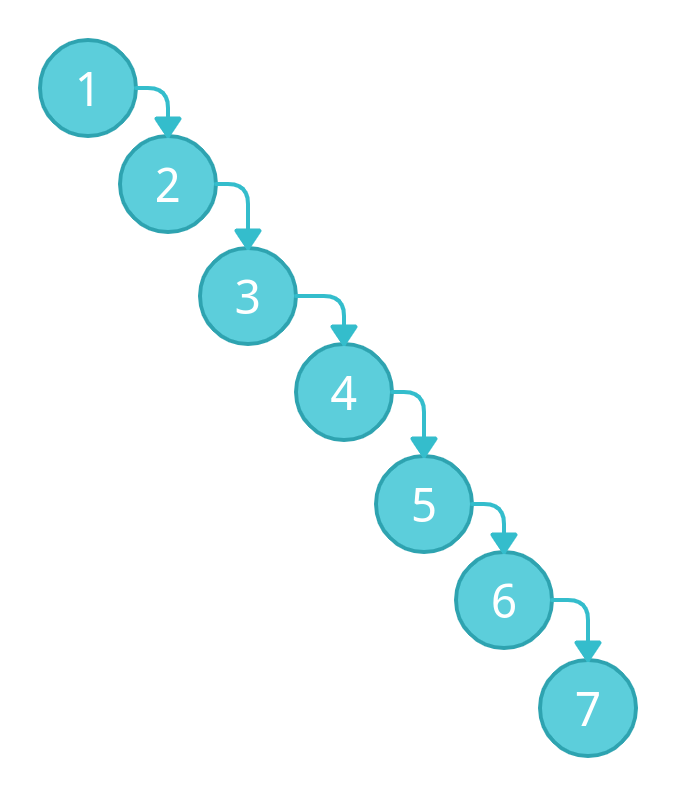
Let's take an example of the above tree which is a valid binary search tree.
👉🏻 Insertion
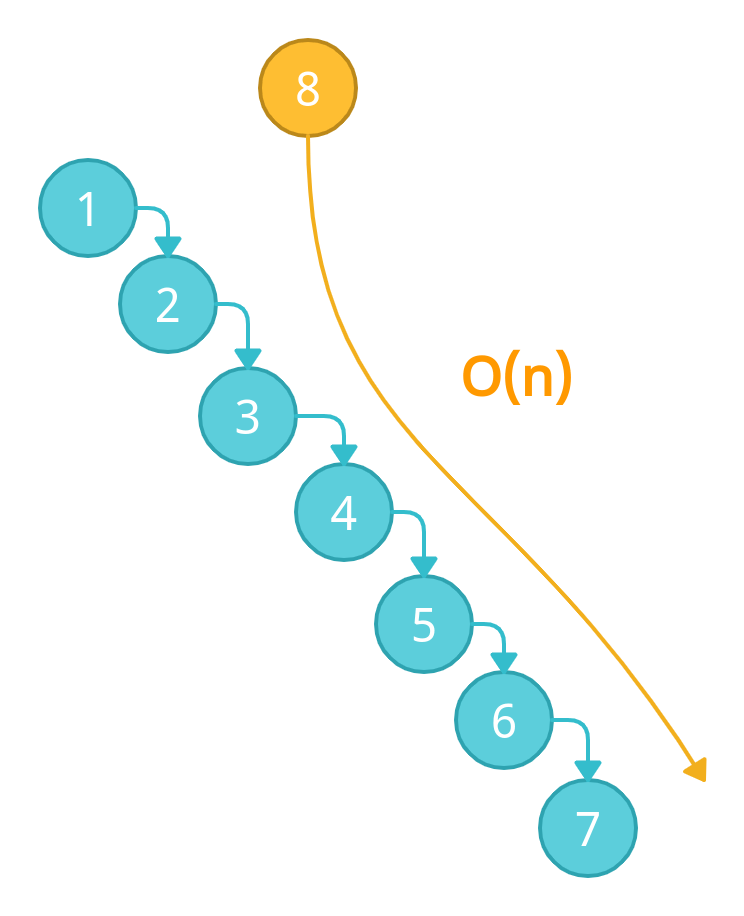
Let's say we want to insert another node 8. According to the rules of BST, it must be inserted as the right child of 1. Therefore, we need to traverse all elements to insert 8 which has the worst case complexity of O(n)
👉🏻 Deletion
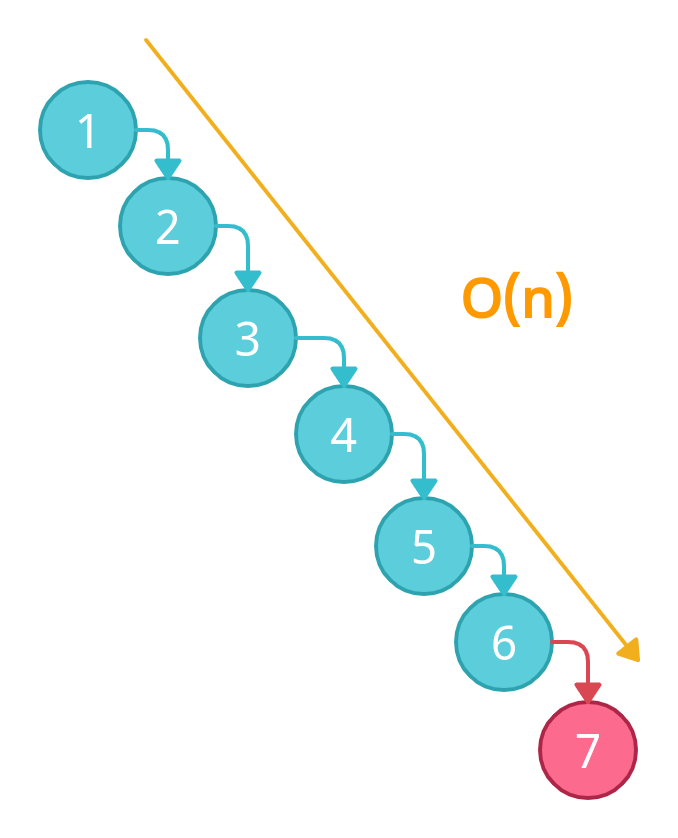
Now, Let's say we want to delete the node 7 from our BST, we have to go down till 7 and delete it. This is also O(n) because we are traversing all the nodes in order.
👉🏻 Searching
For Searching element 7, again we have to traverse all elements. Therefore, searching in a binary search tree has the worst case complexity of O(n).
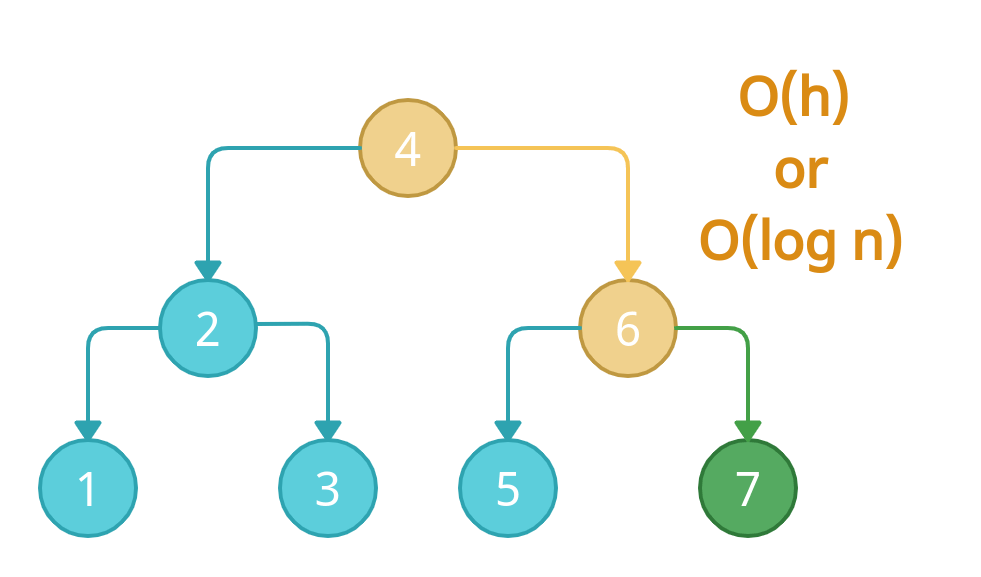
😌 Average Case
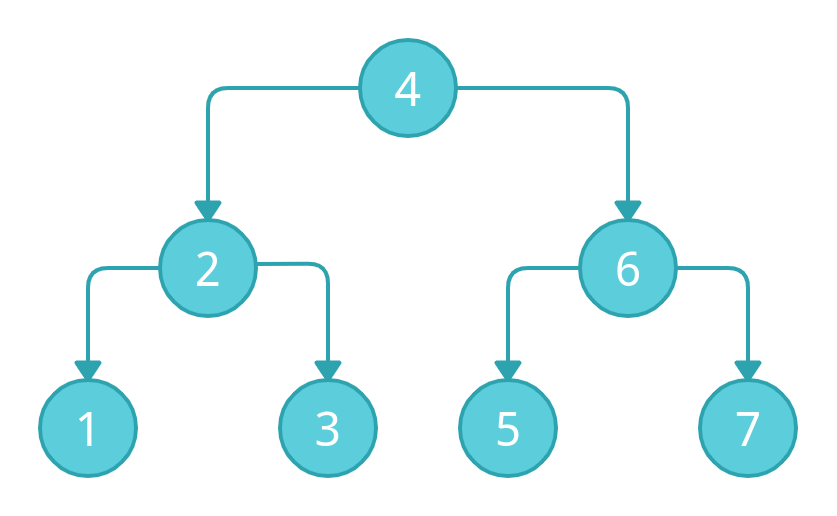
Let's take an example of the above tree which is a perfectly balanced binary search tree. This means the tree is properly divided into sub-trees concerning the data.
👉🏻 Insertion
Let's say, we want to insert another node 8. According to the rules of BST, it must be inserted as the right child of 1. We will traverse the tree and move to the right side of the tree, we found 6, We then go to the right side of the tree again and found 7. Now, there are no nodes to the right of 7, hence we can insert 8 as a right node to it.
In this process, as you can see, we have found the insertion point after 3 checks. That is equal to the height of the tree. Therefore the time complexity of insertion is O(h).
We also use log(n) for it. Let me clear it for you. First, check what is the length of the tree? We will get 7. Perform log base 2 of 7. You'll get 2.8, we can round it off o the nearest digit that is 3. Hence we can say the time complexity can also be O(log n)
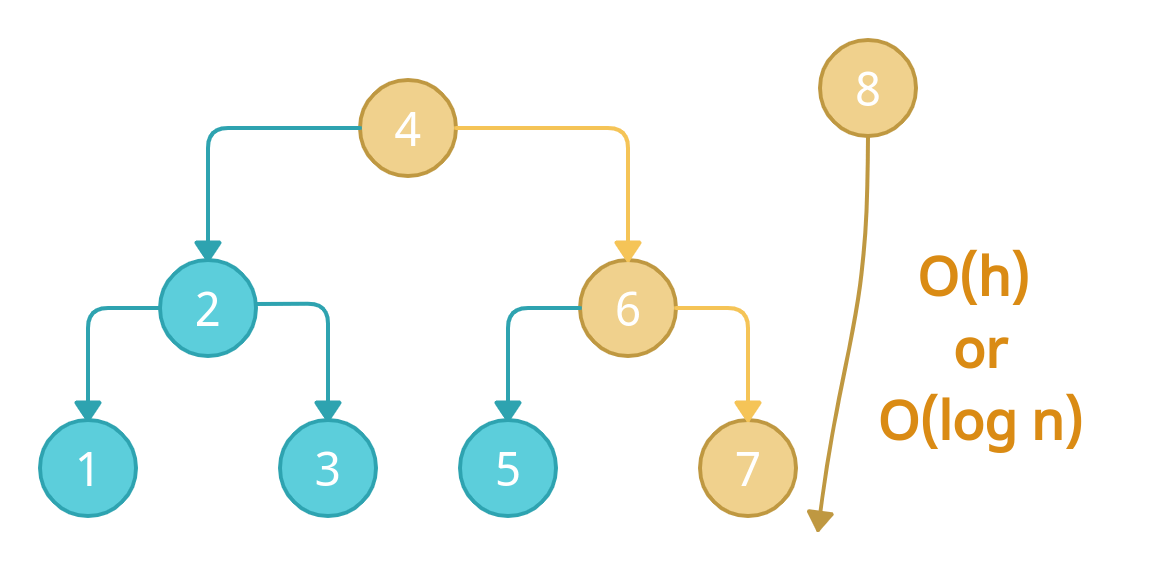
👉🏻 Deletion
The same process goes for the deletion as well. If we want to remove node 7, we can get it by performing three checks and remove it. Hence O(h) or O(log n)
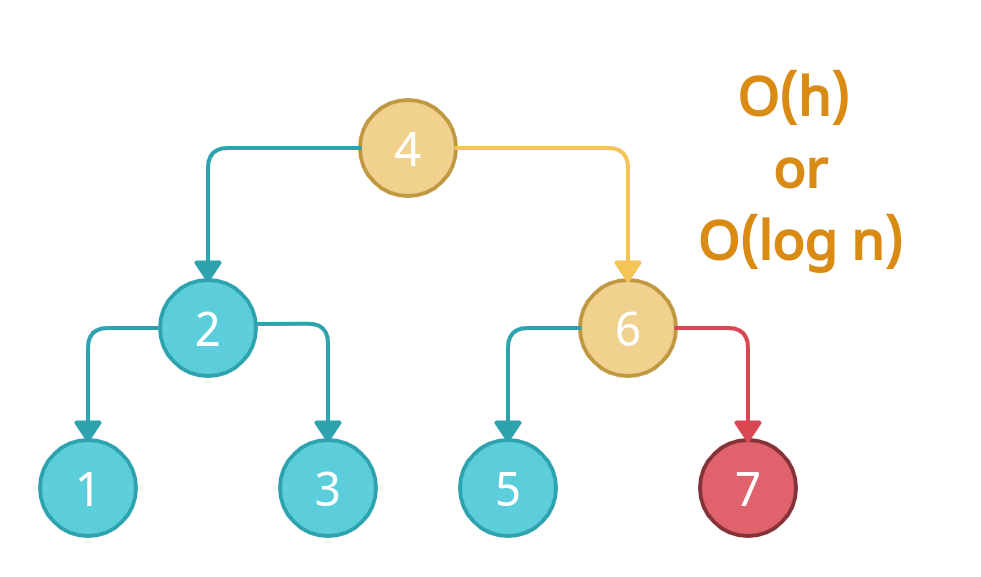
👉🏻 Searching
For Searching element 7, again we have to perform only three checks. Therefore, searching in a binary search tree has the time complexity of O(h) or O(log n)
🌲 Implementation Of Binary Search Using JavaScript
First, we will create a Node class that will represent a particular node in the tree.
Each node will have three properties.
value: The value of the node.left: Left child node.right: Right child node.
class Node {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}
Now, we will create another class BinarySeachTree that is going to represent the tree. This class will hold the reference to the root of the tree. Initially, the root will be null because our tree will be empty.
class BinarySeachTree {
constructor() {
this.root = null;
}
}
Insert
We will create a method insert in our BinarySeachTree class that is going to accept a value as an argument. This value will be the value of the new node that is going to be inserted.
Algorithm
- Create a new node.
- Check if the tree is empty? Set the new node to the
rootnode. - If the tree is not empty, start the tree traversal from the
rootnode. - Check if the node already exists? Then return with a message. Else, proceed.
- Check if the current node value is less than the new node value? Move to left side of the tree.
- Check if the node has a left child?
- If there is no left child, then add the child to the left node.
- Else move to the left node and repeat the process.
- Check if the node has a left child?
- If the current node value is greater than the new node value? Move to the right side of the tree.
- Check if the node has a right child?
- If there is no right child, then add the child to the right node.
- Else move to the right node and repeat the process.
- Check if the node has a right child?
insert(value) {
// create a new node
const newNode = new Node(value);
// if the tree is empty, then set the new node as root node.
if (this.root === null) {
this.root = newNode;
return this;
}
// get the current root node for traversing
let current = this.root;
// start traversing the tree until we have a node
while (current) {
// if the node already exist, return
if (value === current.value) return "node already exist.";
// if the value is less then, move to the left side.
if (value < current.value) {
// do we have the node at left side?
if (current.left === null) {
// if we don't have the node at left,
// set the left node to the new node;
current.left = newNode;
return this;
}
// if there is node to left then
// move to the left node and repeat the process
current = current.left;
} else {
// else, move to the right side.
if (current.right === null) {
// if we don't have the node at right,
// set the right node to the new node;
current.right = newNode;
return this;
}
// if there is node to right then
// move to the right node and repeat the process
current = current.right;
}
}
}
Search
We will create a method search in our BinarySeachTree class that is going to accept a value as an argument. This value will be the value of the node that is going to be searched.
Algorithm
- Check if the tree is empty, return immediately.
- If the tree is not empty, start the tree traversal from the
rootnode. - Check if the current node value is less than the new node value? Move left and repeat the process.
- If the current node value is greater than the new node value? Move right and repeat the process.
- If the node is not at left or right, that means we have found the node because a node can be smaller, bigger, or equal.
- Set the found flag
- Check if we have found the node? Return the node, otherwise, return
undefined.
find(value) {
// if the tree is empty, return
if (!this.root) return false;
// start from the root node
let current = this.root;
// maintain a flag for found or not
let found = false;
// Traverse until
// 1. There are elements
// 2. The node is not found
while (current && !found) {
// if the value is less than the current value
// move to the left side.
if (value < current.value) {
current = current.left;
} else if (value > current.value) {
// if the value is less than the current value
// move to the right side.
current = current.right;
} else {
// if the node is not at left or right, we have found it.
found = current;
}
}
// if the node is not found, return
if (!found) return undefined;
// return the founded node.
return found;
}
Deletion
The deletion in Binary Search Tree has three use cases.
1. The node to be deleted is a leaf node
To delete a leaf node, we simply have to remove it from the tree. Since it was a leaf node, we deleted it from the tree without making any other changes.
2. Node to be deleted has only one child
To delete this node, we first copy the child node, and then delete the node. After that, we make the copied child the new child of the parent.
3. Node to be deleted has two children
In this case, we first find the in-order successor of the node. Then copy the contents of the in-order successor to the node and delete the in-order successor. The in-order predecessor can also be used in the same manner.
We will implement all three cases but the prerequisite to this operation is Recursion
I highly recommend you to watch this video for understanding Recursion: What is Recursion? In Depth
Here is the implementation of the delete operation in the Binary Search Tree:
delete(value) {
this.root = this.deleteNode(this.root, value);
}
deleteNode(root, value) {
// if the root is null, return
if (!root) {
return null;
}
// if the value is less than the current node,
// move to the left side of tree.
if (value < root.value) {
root.left = this.deleteNode(root.left, value);
} else if (value > root.value) {
// if the value is greater than the current node,
// move to the right side of tree.
root.right = this.deleteNode(root.right, value);
} else {
// if the value is equal
// there is no node to left but right has node.
if (!root.left) {
return root.right;
} else if (!root.right) {
// if there is no node to right but left has node
return root.left;
} else {
// if there are two children nodes,
// start finding inorder successor of node;
// get the min to the right. and set the value of node;
root.value = this.getMin(root.right);
// repeat the same process with the sub tree
root.right = this.deleteNode(root.right, root.value);
}
}
return root;
}
// helper method to find the successor node;
getMin(root) {
while (root.left) {
root = root.left;
}
return root.value;
}
I can understand that it's a bit tricky to understand the delete operations, please refer to this amazing video on deleting nodes from binary search tree: Delete a node from Binary Search Tree( Reason for every operation explained)
That's it, folks! hope it was a good read for you. Thank you! ✨

