Data Structures 101: Tree Traversal - DFS (Pre, In & Post)
A simple and visual guide for you to understand Tree Traversal using DFS techniques like Pre, In, and Post order.
Assalam u Alaikum & Hello everyone! 👋
In the previous article, we learned about Binary Search Trees. In this article, we will learn how we can traverse a tree using the DFS technique.
Prerequisite
1. Recursion
Traversing a tree requires a good understanding of how Recursion works. Because implementations of tree traversals with iterative approaches are very difficult to learn and elaborate as well. Recursion makes it easy. Therefore, I highly recommend you to watch these videos if you don't have any idea what the recursion is.
2. Binary Tree
Understanding the binary tree is also helpful because we will implement the tree traversals for the binary tree. You can read my previous two articles to understand the trees and binary trees.
First, Let's Create A Binary Tree
Let's create a small binary tree using an approach that is not recommended but will work fine for our lesson today.
Let's create a class Node which will hold three properties:
value- The value of the node.left- The left child.right- The right child.
class Node {
constructor(value) {
this.value = value;
this.right = null;
this.left = null;
}
}
Now we have the node, let's create a binary tree using the node class.
/*
Example Tree:
1
/ \
2 3
/ \ / \
4 5 6 7
*/
const binaryTree = new Node(1);
/**
* Please note that this is a hacked version of binary tree 😂
* => Not scalable, and maintainable
But good for the sake of learning Traversals.
* => Please feel free to use any implementation.
* => The focus of this post is on the traversal
*/
binaryTree.left = new Node(2);
binaryTree.right = new Node(3);
binaryTree.left.left = new Node(4);
binaryTree.left.right = new Node(5);
binaryTree.right.left = new Node(6);
binaryTree.right.right = new Node(7);
🌲 Tree Traversal using DFS
Tree traversal means visiting every node of the tree at least once. DFS (Depth First Search) is a technique in which we traverse a tree in depth. Whenever we visit any node, we first visit all the children of that node and then move forward with other nodes.
We can perform a DFS using three ways:
- Pre Order Traversal
- Post Order Traversal
- In Order Traversal
Let's take a look at them one by one.
🌲 Pre Order Traversal
In a pre-order traversal, the traversing is performed from the Root to the complete left sub-tree and then the complete right sub-tree.
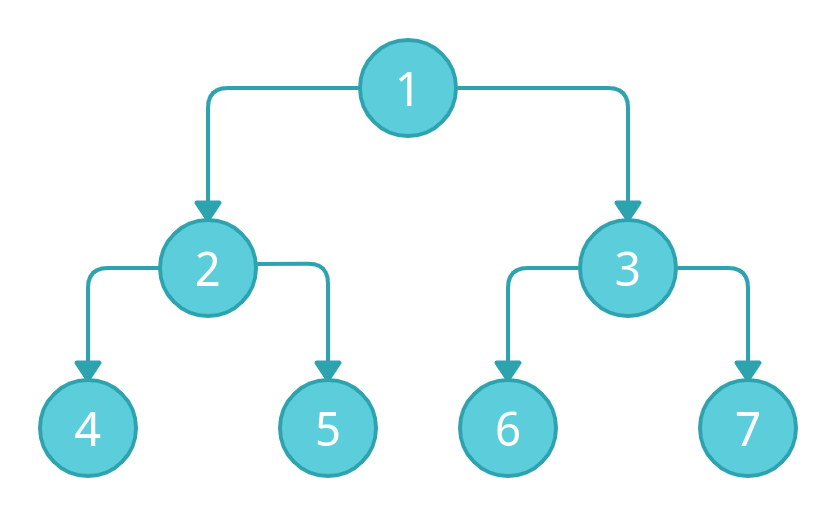
Suppose, we have the above tree and we have to perform the pre-order traversal.
We will start the traversal from node 1. Then we will go to the left sub-tree, and the next node will be 2. Then again, we will go to the left sub-tree, so the next node will be 4. Now, again we will check do we have another left node ahead?
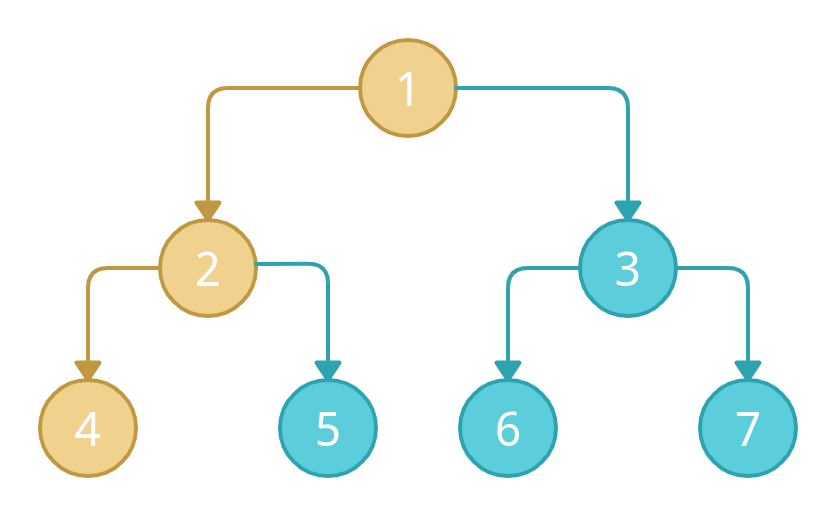
Since node 4 doesn't have any left or right node, we will backtrack (grey nodes) to the parent node 2. We will check if node 2 has any right child? In our case, we have the right child 5, so the next node will be node 5.
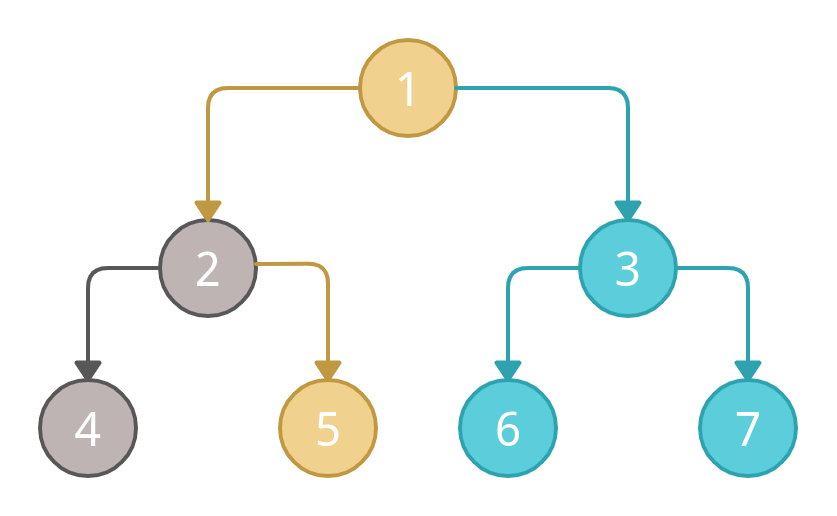
We have traversed, node 2 completely, and now we will backtrack to the parent node, and repeat the process.
Now, we don't have any node left in the left sub-tree, we will backtrack to the root node 1 and repeat the same process for the right sub-tree now.
Again, as per the traversing order (Root, Left, Right), we will traverse the left side of the right sub-tree first. Therefore, marking the nodes 3 and 6 as visited.
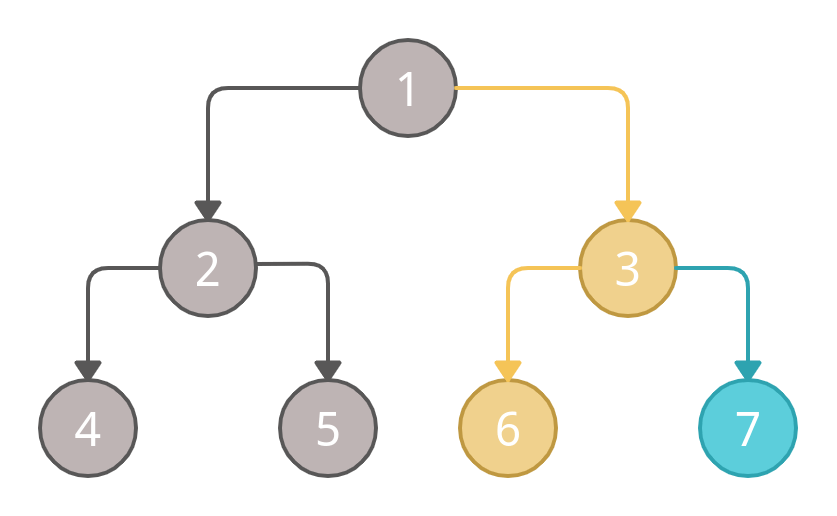
At last, we will mark node 7 as visited.
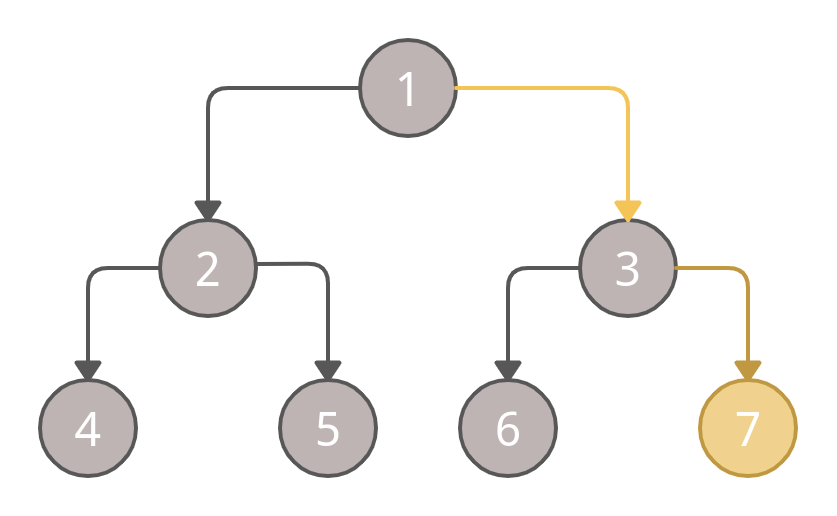
So the order of traversal of the right sub-tree will be: 3, 6 and 7
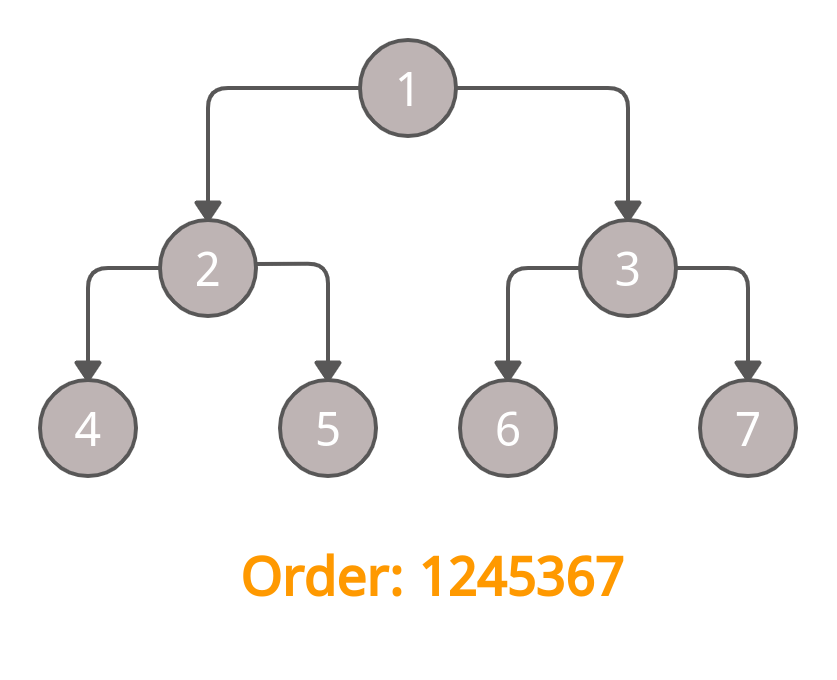
Pre Order Output: 1245367
// accept the starting point as root.
const preOrderTraversal = (root) => {
// base case for recursion, if there is no root, then return.
if (!root) return;
// print the root. You can also store it or do anything else here.
console.log(root.value);
// repeat the same process for the left subtree
preOrderTraversal(root.left);
// after completing the left sub-tree, complete the right sub-tree
preOrderTraversal(root.right);
};
🌲 In Order Traversal
In an in-order traversal, the traversing is performed from the complete left sub-tree to the Root and then the complete right sub-tree.
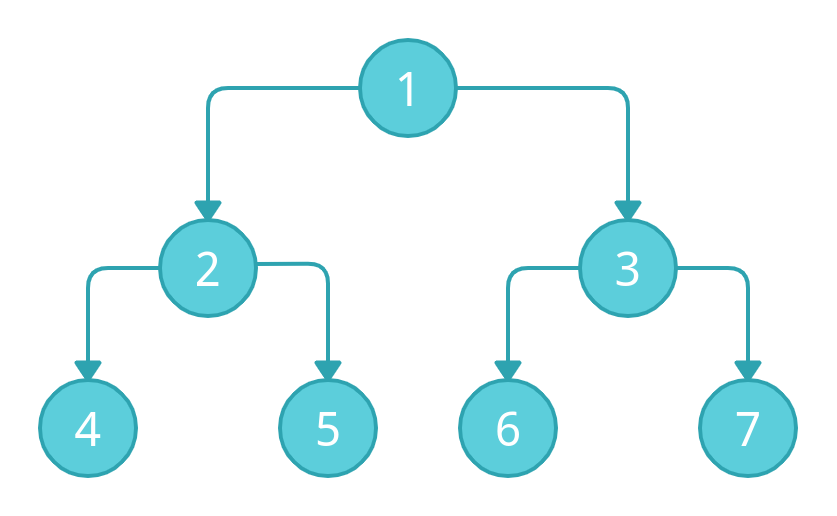
Suppose, we have the above tree and we have to perform the in-order traversal.
We will start the traversal from node 1. But we will not mark this node visited yet.
Remember, we have to start the actual traversal from the left sub-tree. Therefore, we will go to the left node 2. Node 2 has another left node 4, we will move to 4. Again, we will check if node 4 has any left node? In this case, we don't have any other left node. Therefore, we will start the actual traversal from here.
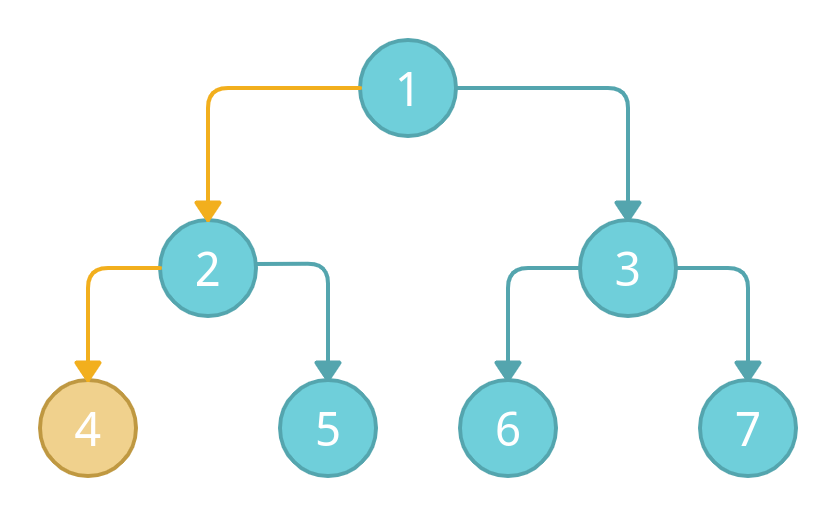
We will mark 4 as visited, then backtrack to node 2 and mark it as visited. After node 2, we will mark node 5 as visited which is the right child of node 2.
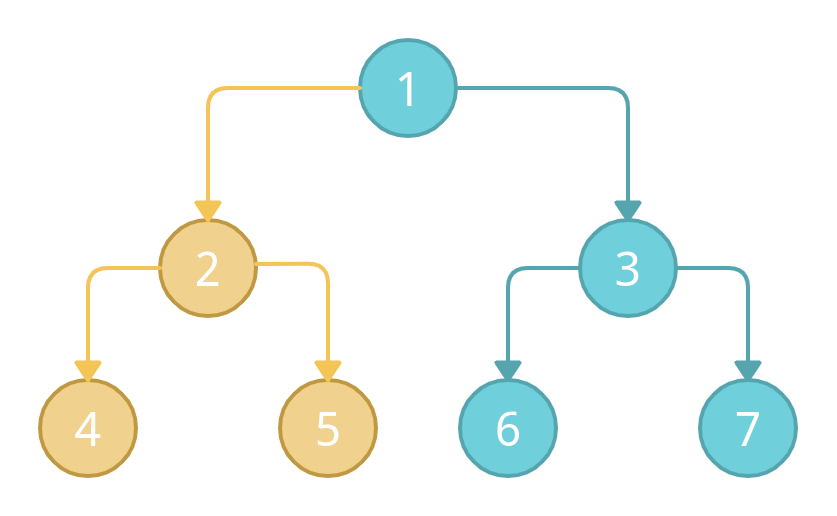
Now, we have visited the left subtree of the root node completely, and we will backtrack to the root. We will mark the root node 1 as a visited node and will jump to the right subtree and visit its node again from the bottom leaf nodes to the upward nodes.
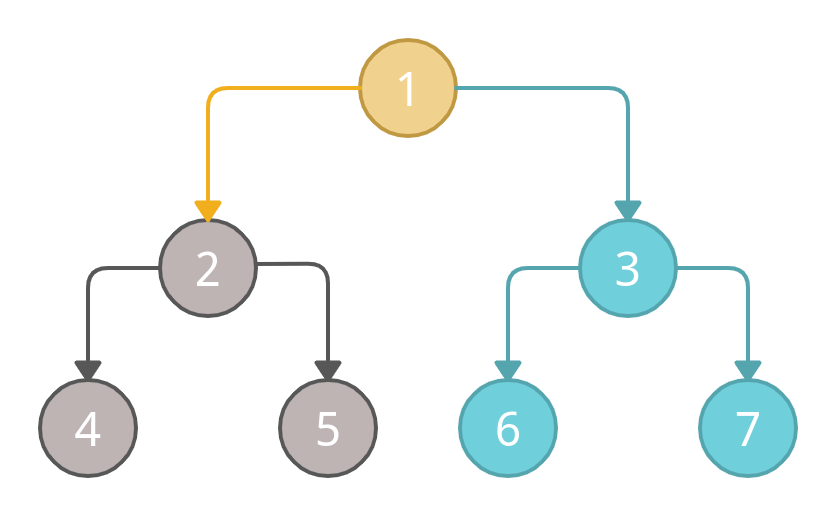
After visiting node 1, we have successfully traversed the left sub-tree and the parent, now we will move to the right sub-tree.
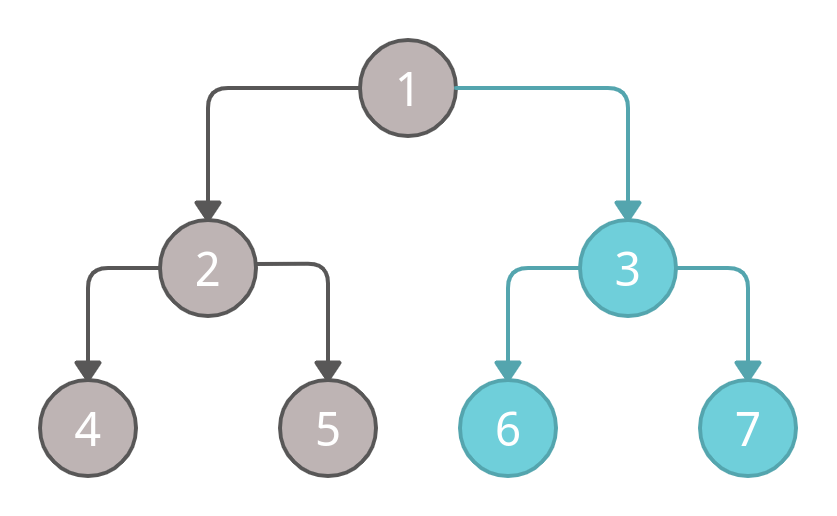
Now, we will use the same order to traverse the right sub-tree. We will start from the left side and mark node 6 as visited.
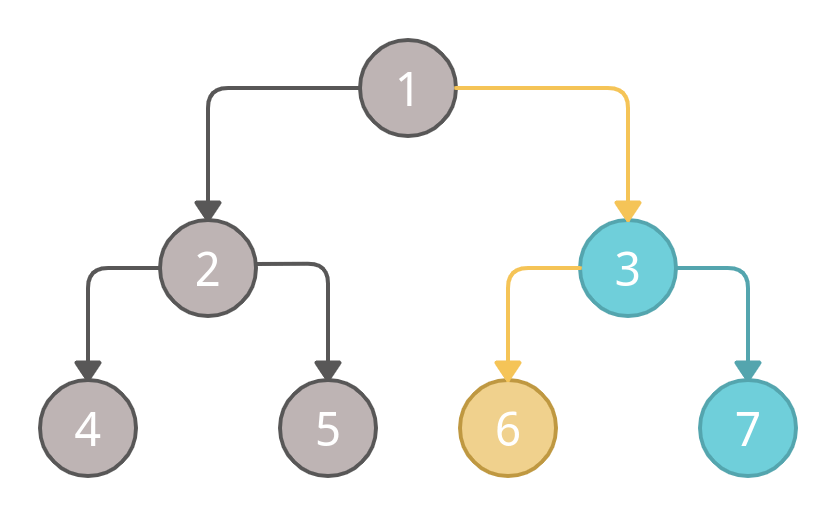
After that, we will move to the parent node i.e node 3, and mark it as visited.
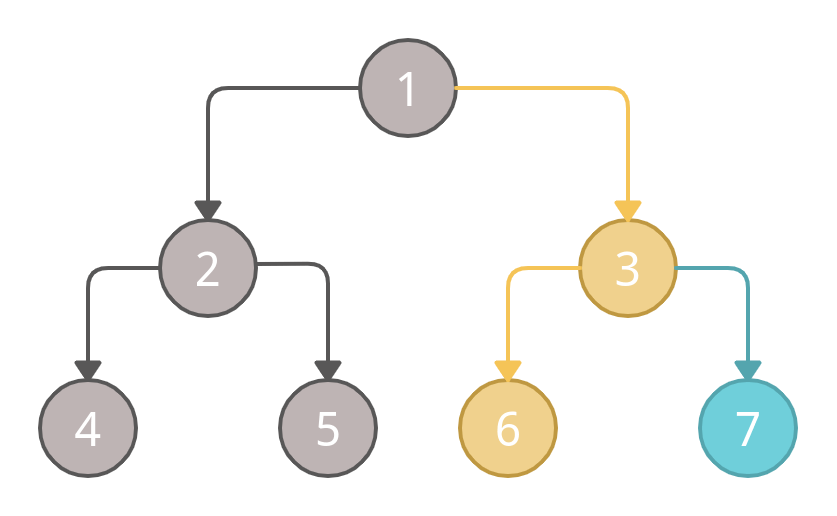
At last, we will mark the node 7 as visited
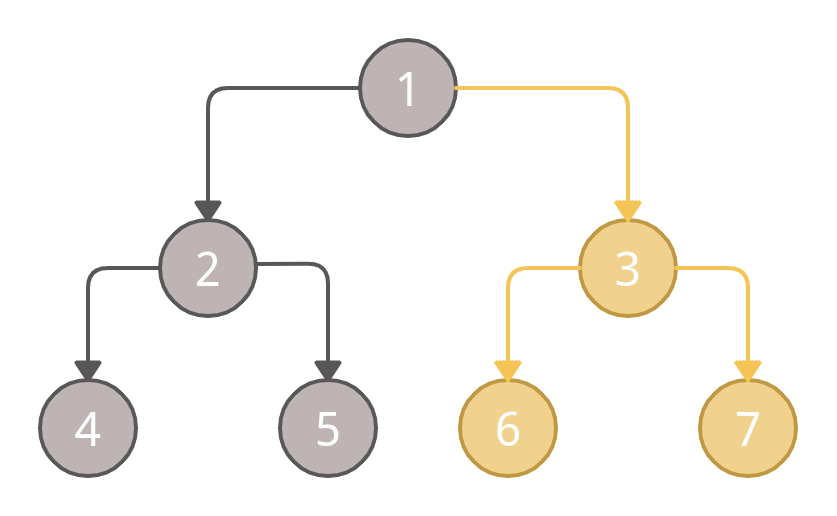
We will mark the node 7 and complete the traversal.
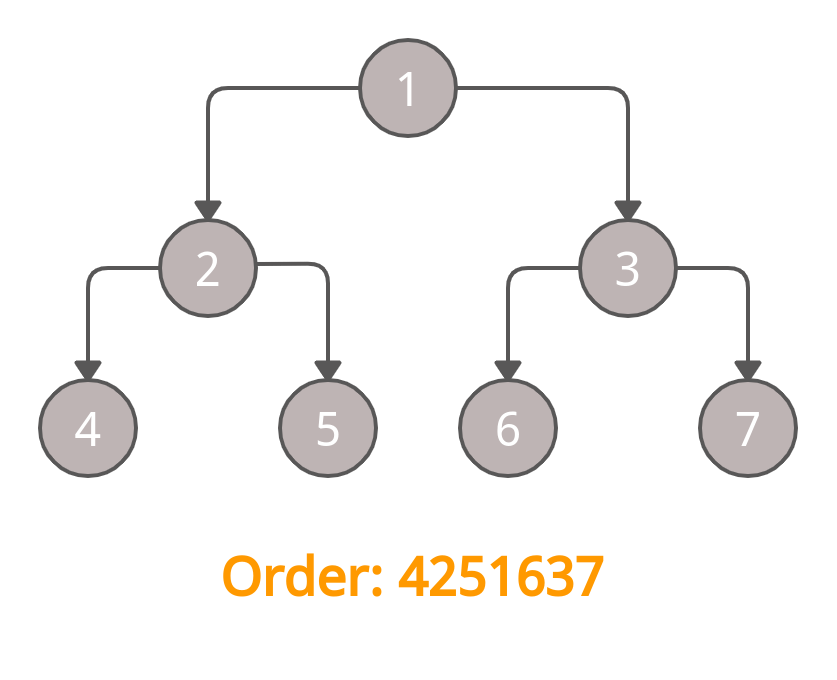
In Order Output: 4251637
// accept the starting point as root.
const inOrderTraversal = (root) => {
// base case for recursion, if there is no root, then return.
if (!root) return;
// first, traverse the left sub-tree
inOrderTraversal(root.left);
// print the root
console.log(root.value);
// at last, traverse the right sub-tree
inOrderTraversal(root.right);
};
🌲 Post Order Traversal
In a post-order traversal, the traversing is performed from the complete left sub-tree, then the right sub-tree, and at last the root.

Suppose, we have the above tree and we have to perform the post-order traversal.
We will start from the root node 1 but not mark it visited as we did in the in-order traversal. We will jump to the left sub-tree and start the traversal from the leaf node in the left sub-tree.
Node 1 has left child node 2 which has a left child node 4. Node 4 is also a leaf node (without children). Therefore, we will mark node 4 as a visited node.
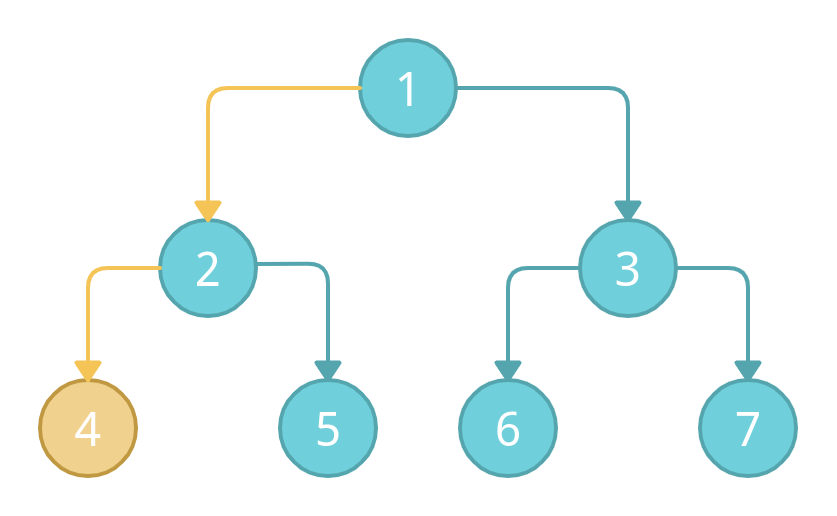
Then we will come to node 2 again, and check if it has any right node? Yes, it has node 5 as the right child. Therefore, mark node 5 as visited.
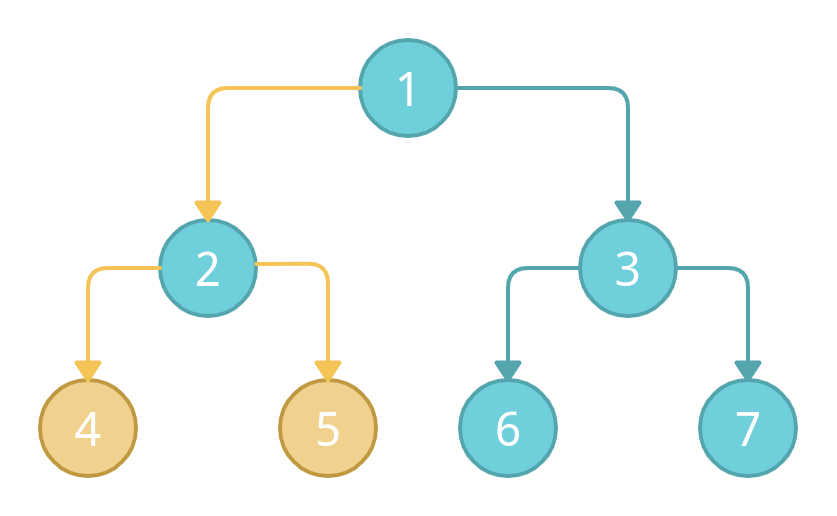
Now according to the pattern, we have visited the left and right nodes. Now we will mark the parent node 2 as visited.
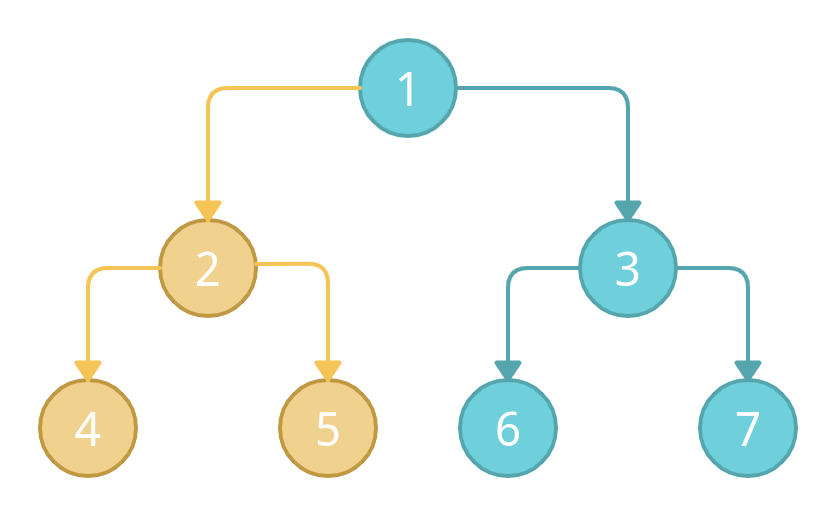
We have completed the left sub-tree traversal for node 1 (root node). Now we will start the right sub-tree traversal.
For the right sub-tree, we will repeat the Left, Right, and Root pattern again. For the right sub-tree, the root node is 3 and it has a left node 6 and a right node 7.
We will mark node 6 as visited first according to the pattern.
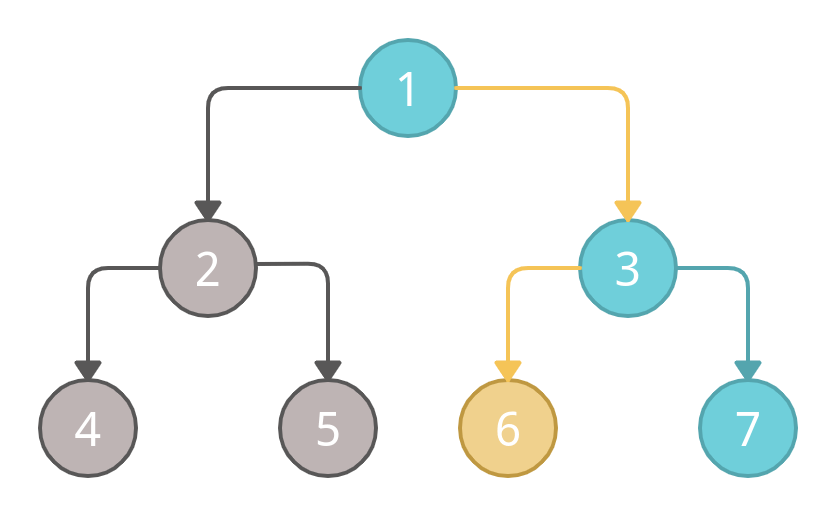
After it, we will mark node 7 as visited.
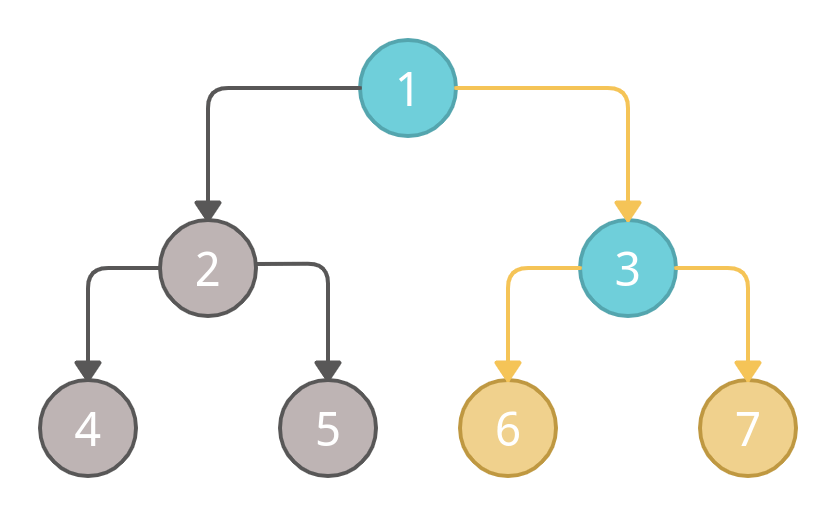
At last, we will mark the node 3 (root node of right sub-tree) as visited.
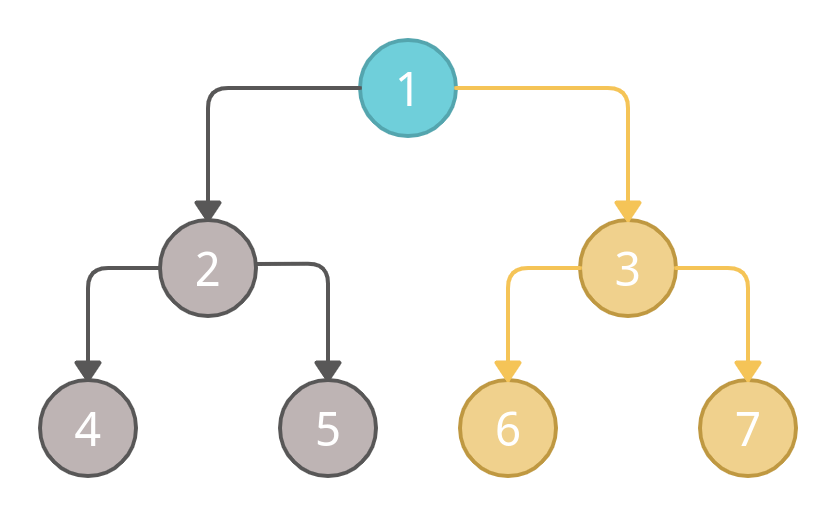
Now we have visited the left and right sub-trees of root node 1, we will mark the root node 1 as visited now.
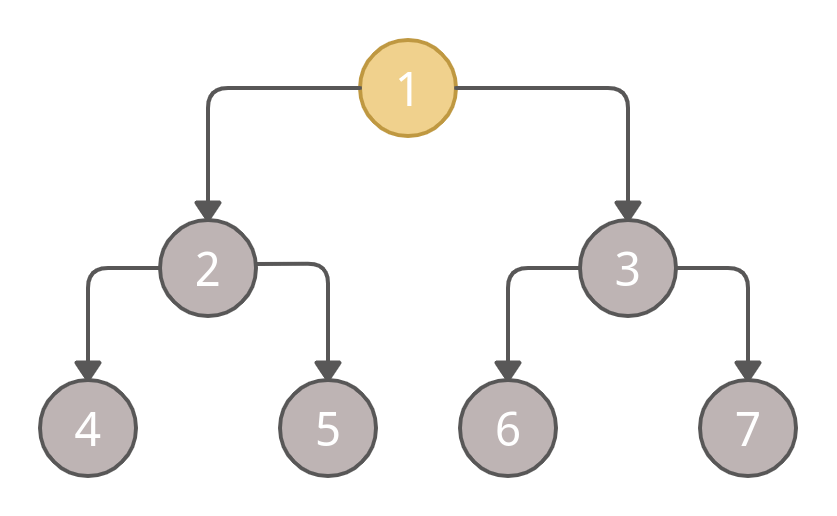
After marking node 1 as visited, we have completed the traversal using the Post Order Traversal technique.
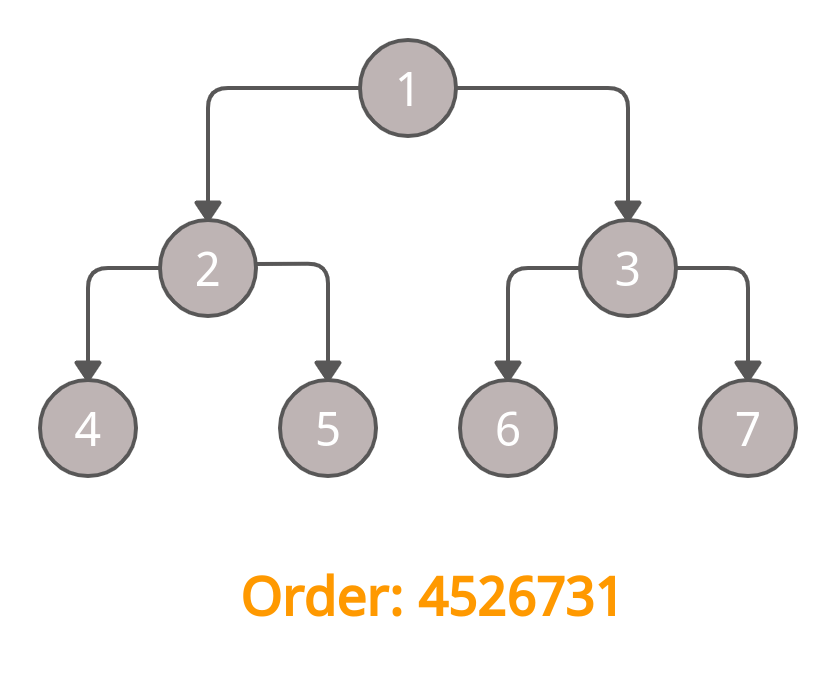
Post Order Output: 4526731
// accept the starting point as root.
const postOrderTraversal = (root) => {
// base case for recursion, if there is no root, then return.
if (!root) return;
// first, traverse the left sub-tree
postOrderTraversal(root.left);
// then traverse the right sub-tree
postOrderTraversal(root.right);
// at last, print the root
console.log(root.value);
};
That's it, folks! hope it was a good read for you. Thank you! ✨

