Assalam u Alaikum & Hello everyone! 👋

In the previous article, we learned about Tree Traversals and how to traverse a tree using the Depth First Search (DFS) Technique. We also learned the three techniques (Pre Order, In Order & Post Order) which we use in DFS.

In this article, we will learn how we can traverse a tree using the Breadth First Search BFS technique.

🌲 Tree Traversal using BFS

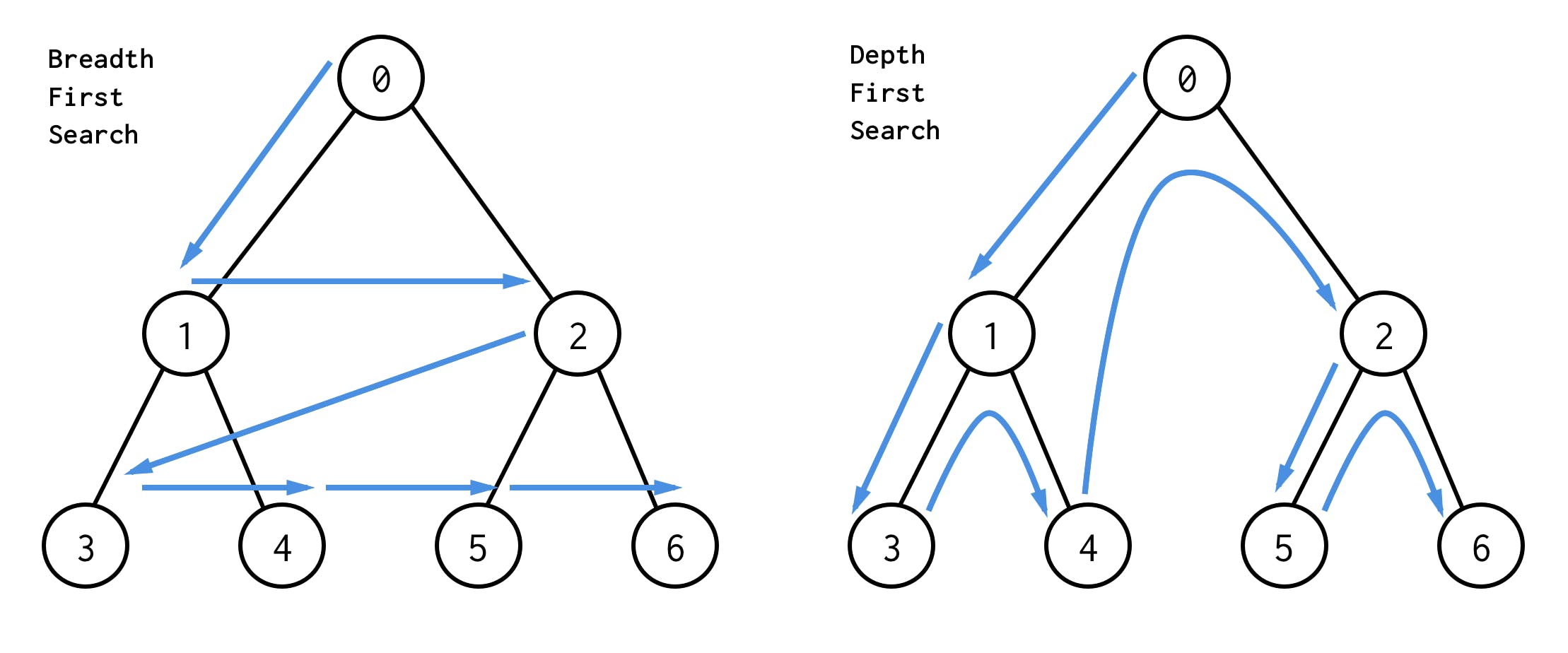
In BFS, we traverse the tree in level order which means that we first visit the nodes of level 1, then all the nodes of level 2, and so on till level N. In DFS, we traverse the tree in-depth, but in BFS, we traverse the tree concerning the levels of the tree.

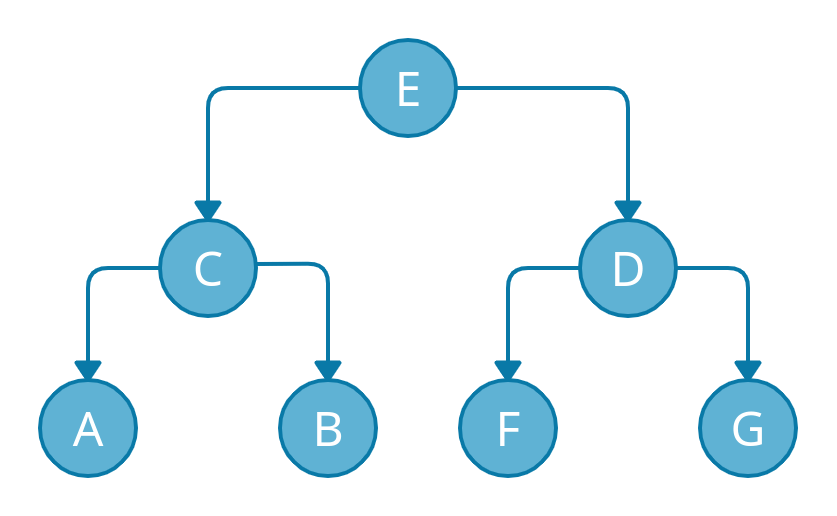
Suppose we have the following tree and we want to traverse it using the BFS technique. We have a total of 3 levels in this tree.

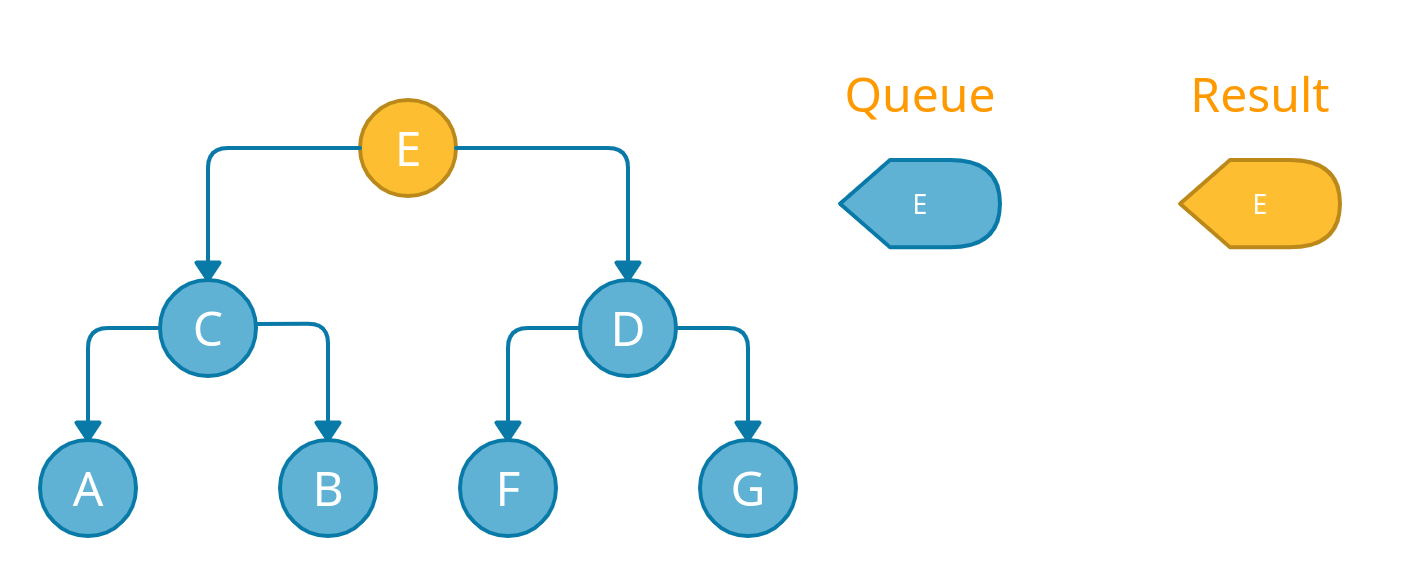
First, we will start the traversal from the root node E. We use a queue to keep track of what nodes we have to visit next.

When we will visit node E, we will do four things.

1. Push the node E into the queue.
2. Mark the node E visited.
3. Check if the node E has any left child then push it to the queue. Also, check if the node E has any right child then push the right child into the queue as well.
4. Remove the node E from the queue and move to the next item into the queue.

Let's understand the steps one by one.

First, we will push the node E into the queue and mark E as visited.

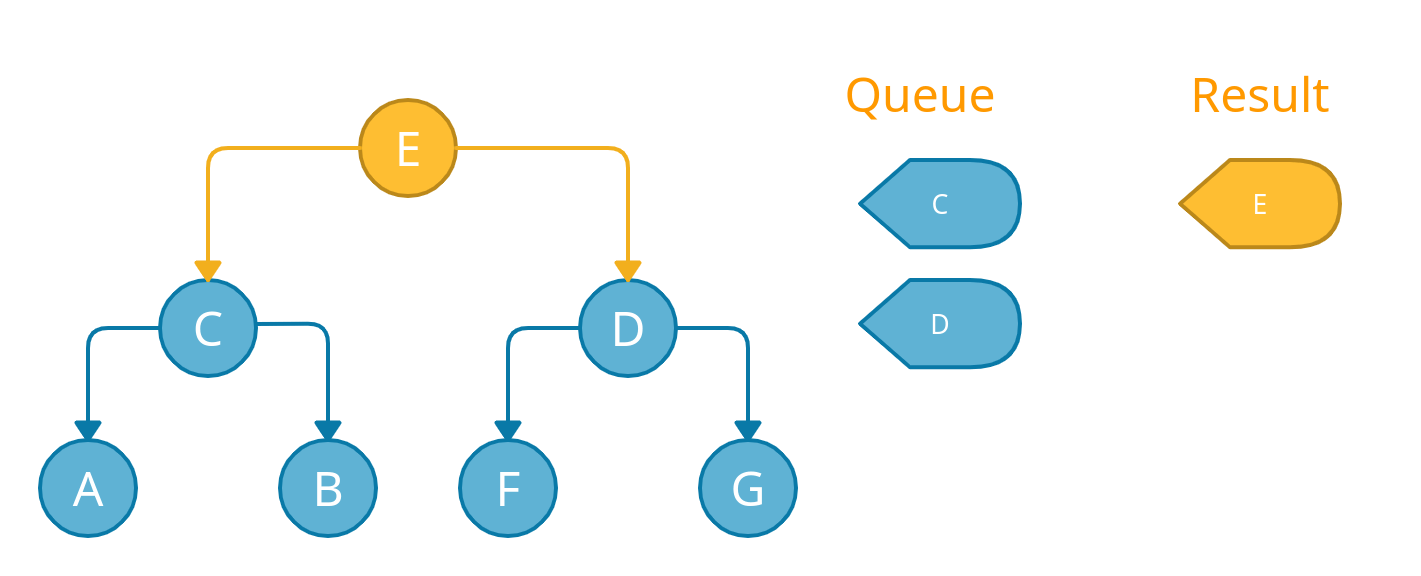
After that, we will check if node E has a left child? if yes then we will push the left child into the queue. Same for the right child.

Since node E has both left and right children, we will push both of them into the queue and remove node E from the queue because it's already visited.

This will complete the level 1 traversal of the tree.

Next, we will repeat the same four steps for the next item in the queue.

The next node in the queue is C, we will mark the node C as visited, push its left and right child into the queue, and remove it from the queue.

The next node, in the queue, is node D. Again, we will mark the node D as visited, push its children into the queue and remove it from the queue.

This will complete the level 2 traversal of the tree.

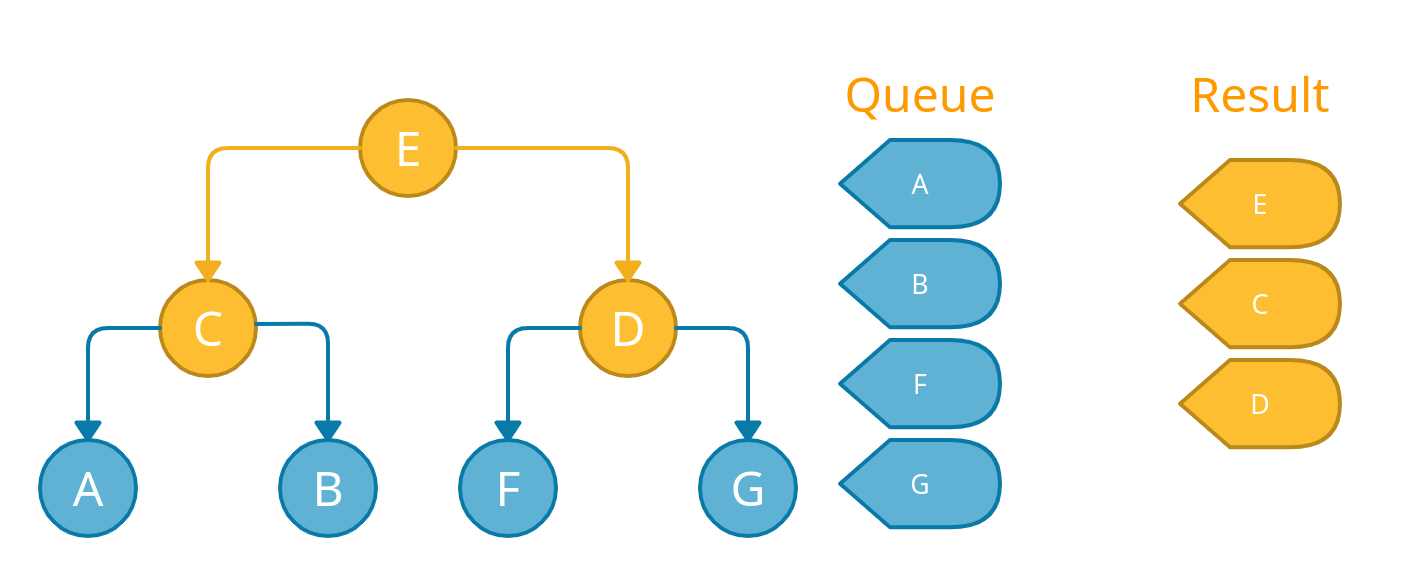
We will repeat the same process for the node A and B. Since A and B don't have any children, we will not push anything into the queue. We will mark them visited and then remove them from the queue just as we did with other nodes.

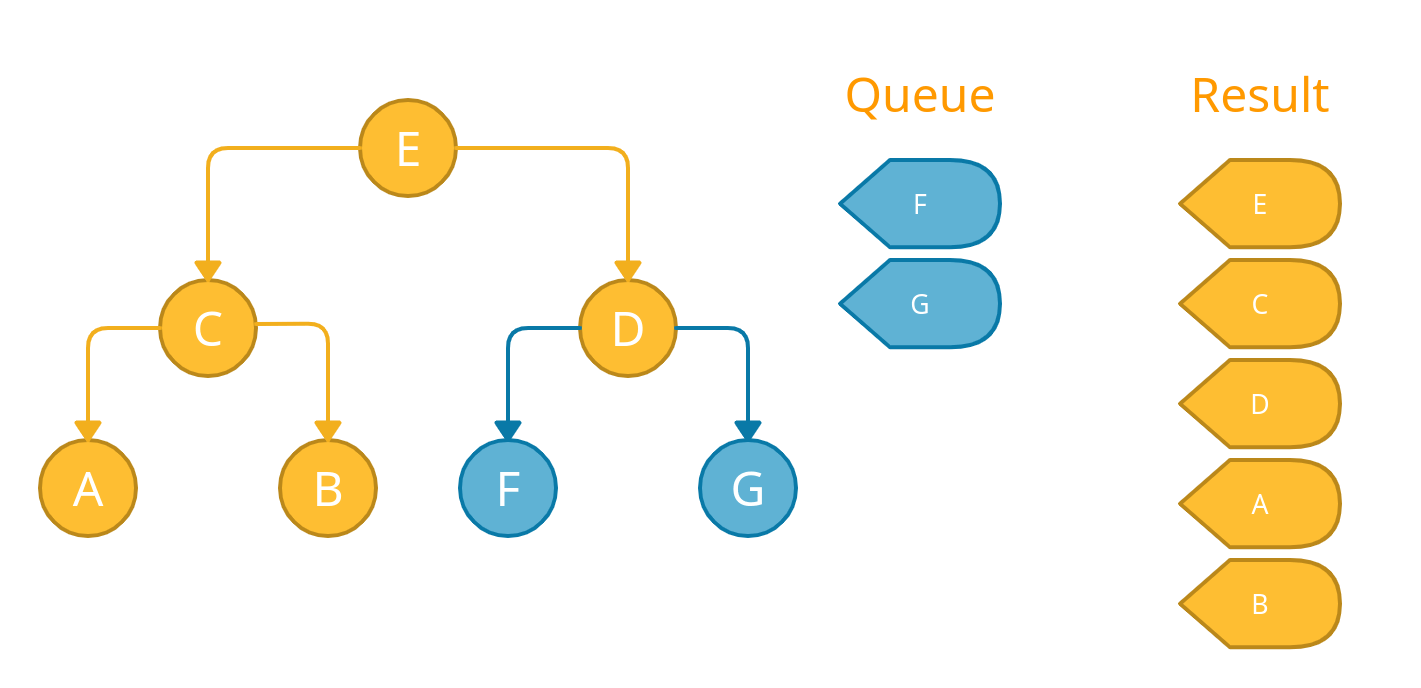
Now we have the last two nodes remaining in the queue, we will perform the same operations for them again one by one.

This will complete the level 3 traversal of the tree.

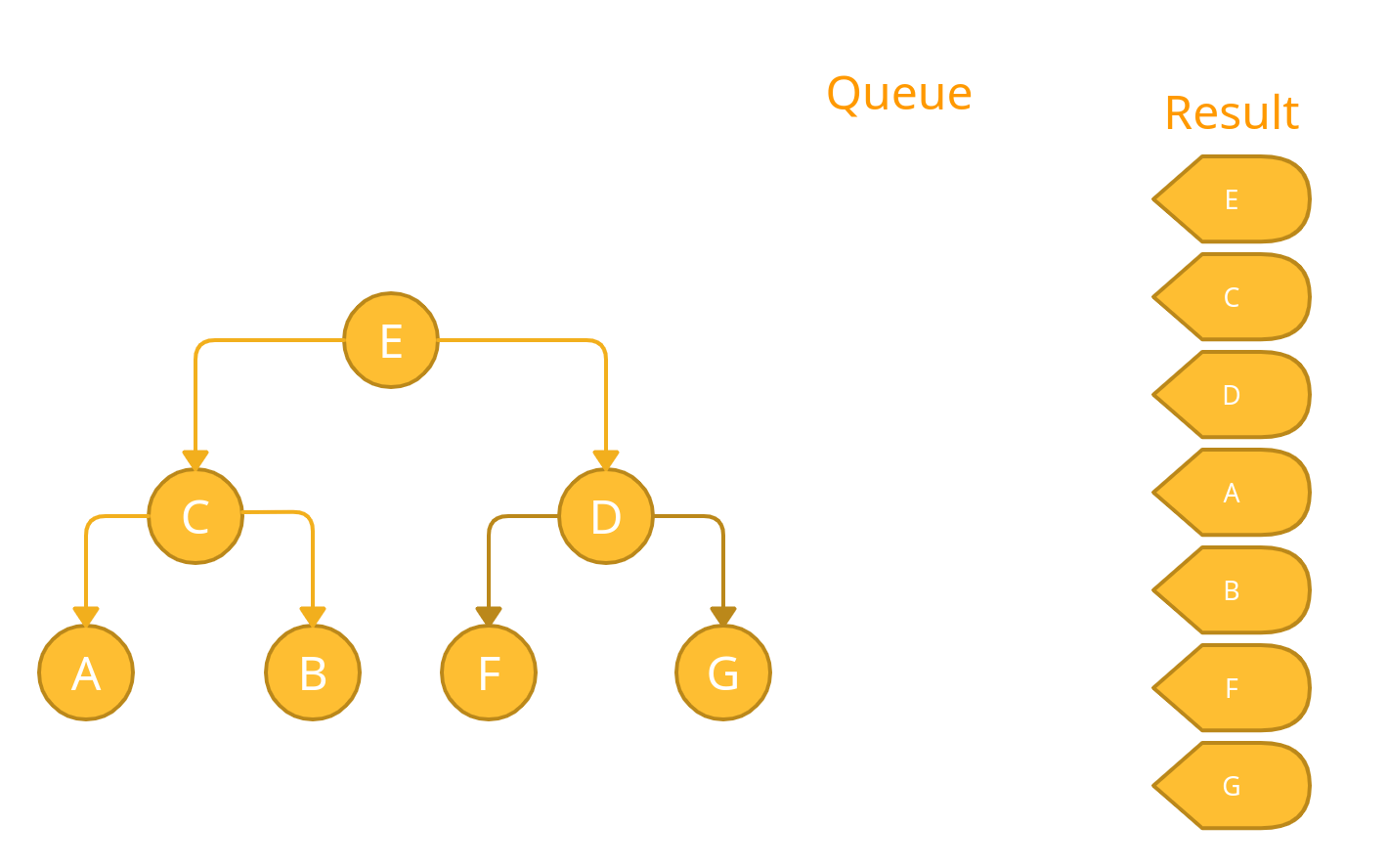
At last, we have an empty queue, which means that we have completed the traversal 🚀

Traversal Order: E C D A B F G

🌲 Implentation of BFS in JavaScript

Let's create a small binary tree using an approach that is not recommended but will work fine for our lesson today.

Let's create a class Node which will hold three properties:

1. value - The value of the node.
2. left - The left child.
3. right - The right child.

class Node {
  constructor(value) {
    this.value = value;
    this.right = null;
    this.left = null;
  }
}

Now we have the node, let's create the same binary tree using the node class.

const binaryTree = new Node("E");
binaryTree.left = new Node("C");
binaryTree.right = new Node("D");
binaryTree.left.left = new Node("A");
binaryTree.left.right = new Node("B");
binaryTree.right.left = new Node("F");
binaryTree.right.right = new Node("G");

Let's create a function for BFS traversal. I'm naming it BFS, you can name anything you want.

// accept the first node as an argument.
const BFS = (root) => {
  // if the node is null, return
  if (!root) return;
  // create a queue, and push the first element inside it.
  const queue = [root];
  // create a result to hold the result
  const result = [];
  // Loop over the queue, until it has nodes
  while (queue.length > 0) {
    // get the front of the queue (active node)
    const node = queue[queue.length - 1];
    // push the node into result (mark visited)
    result.push(node.value);
    // check if it has any left child? If yes, the enqueue
    if (node.left) queue.unshift(node.left);
    // check if it has any right child? If yes, the enqueue
    if (node.right) queue.unshift(node.right);
    // dequeue from the queue
    queue.pop();
  }
  return result;
};

Let's test our implementation now.

console.log(BFS(binaryTree)); // ["E", "C", "D", "A", "B", "F", "G"]

---

That's it, folks! hope it was a good read for you. Thank you! ✨

👉 Follow me: Github Twitter LinkedIn Youtube